Graph Depth-First Search (DFS)
A while ago, I have written up on Graphs and gave a few examples about their application for real world problems. In this post, I want to talk about one of the most common graph algorithms, Depth-first search (DFS).
28 July 2018
2 minutes read
Related Posts
A while ago, I have written up on Graphs and gave a few examples about their application for real world problems. I absolutely love graphs as they are so powerful to model the data for several key computer science problems. In this post, I want to talk about one of the most common graph algorithms, Depth-first search (DFS) and how and where it could be useful.
What is Depth-First Search (DFS)?
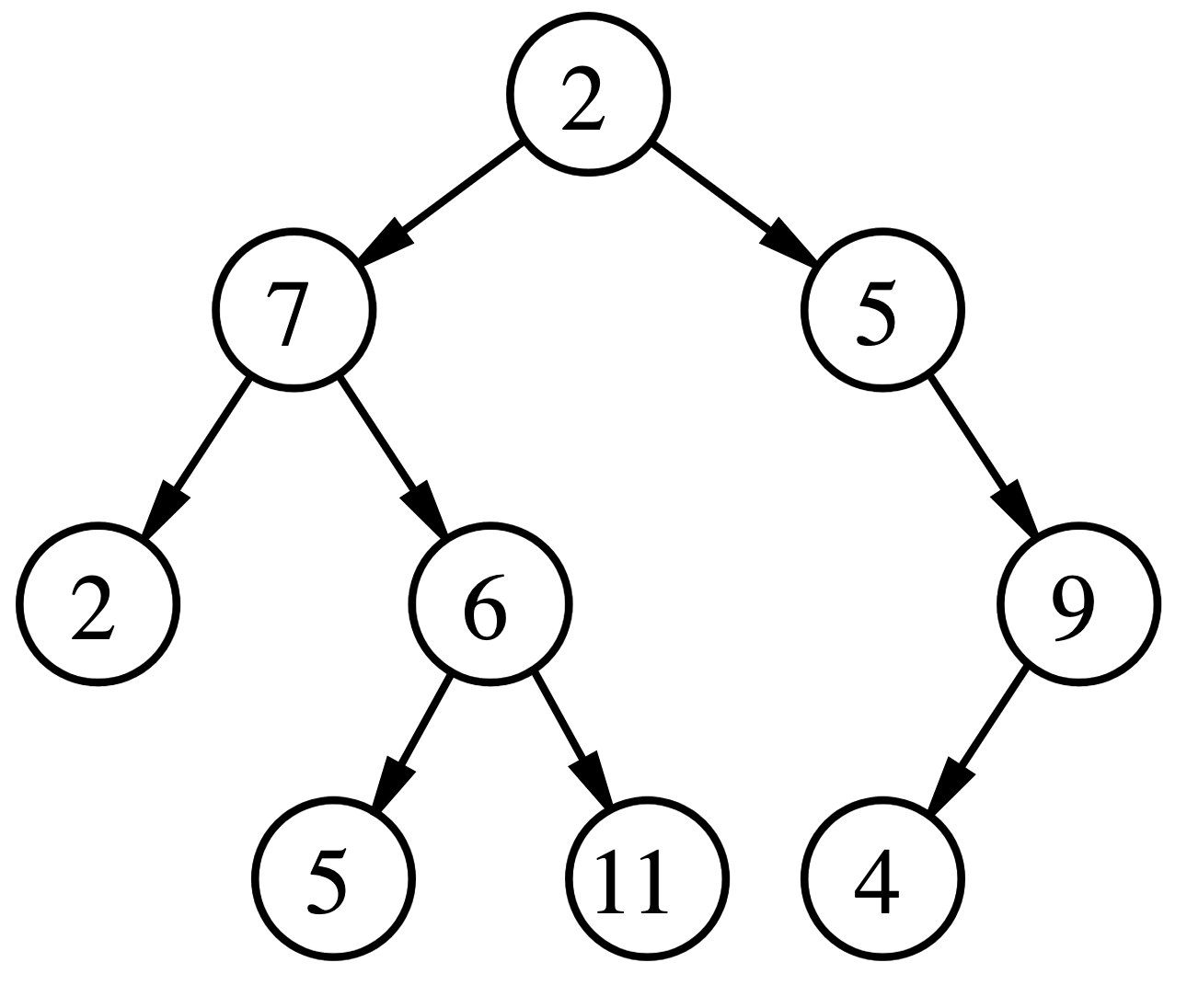
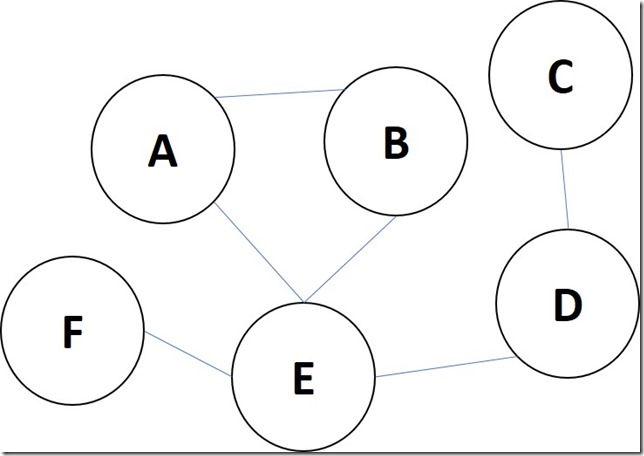
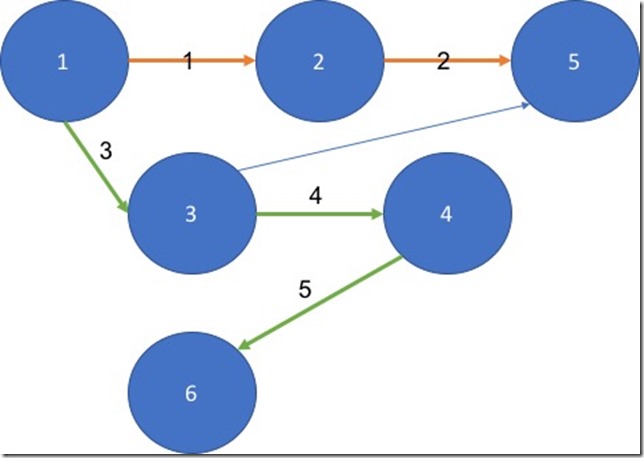
DFS is a specific algorithm for traversing and searching a graph data structure. Depending on the type of graph, the algorithm might differ. However, the idea is actually quite simple for a Directed Acyclic Graph (DAG):
- You start with a source vertex (let's call it "S")
- You visit the first neighbour vertex of that node (let's call this "N")
- You do the same for "N" and you keep going till you end up at a leaf vertex (L) (which is a vertex that has no edges to another vertex)
- Then you visit the second neighbour of L's parent vertex.
- You would be once you exhaust all the vertices.
I must admit that this is a bit simplified version of the algorithm even for a DAG. For instance, we didn't touch on the fact that we might end up actually visiting the same vertex multiple times if we don't take this into account in our algorithm. There is a really good visualization of this algorithm here where you can observe how the algorithm works in a visual way through a logical graph representation.
Application of Depth-First Search
There are various applications of DFS which are used to solve particular problems such as Topological Sorting and detecting cycle in a graph. There are also occasions where DFS is used as part of another known algorithm to solve a real world problem. One example to that is the Tarjan’s Algorithm to find Strongly Connected Components.
This is also a good resource which lists out different real world applications of DFS.
Other Graph Traversal Algorithms
As you might guess, DFS is not the only known algorithm in order to traverse a graph data structure. Breadth-First Search (BFS) is a another most known graph traversal algorithm which has the similar semantics to DFS but instead of going in depth on a vertex, it prefers visit the all the neighbors of the current vertex. Bidirectional search is another one of the traversal algorithms which is mainly used to find a shortest path from an initial vertex to a goal vertex in a directed graph.
Hey, I'm Tugberk 👋
Coder 👨🏻💻, Speaker 🗣, Author 📚, ex-Microsoft MVP 🕸, Blogger 💻
I live in London, UK 🏡
